Solved

Use the Following to Answer Questions

Question 63

Multiple Choice

Use the following to answer questions :
p(x) = x4 - 5x3 + 5x2 + 5x - 6
-Use the rational roots theorem to list all possible rational roots.


A) Use the following to answer questions : p(x) = x<sup>4</sup> - 5x<sup>3</sup> + 5x<sup>2</sup> + 5x - 6 -Use the rational roots theorem to list all possible rational roots. A) B) C) D)
B) Use the following to answer questions : p(x) = x<sup>4</sup> - 5x<sup>3</sup> + 5x<sup>2</sup> + 5x - 6 -Use the rational roots theorem to list all possible rational roots. A) B) C) D)
C) Use the following to answer questions : p(x) = x<sup>4</sup> - 5x<sup>3</sup> + 5x<sup>2</sup> + 5x - 6 -Use the rational roots theorem to list all possible rational roots. A) B) C) D)
D) Use the following to answer questions : p(x) = x<sup>4</sup> - 5x<sup>3</sup> + 5x<sup>2</sup> + 5x - 6 -Use the rational roots theorem to list all possible rational roots. A) 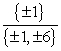B) 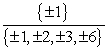C) 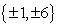D)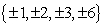

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q58: Use synthetic division and the remainder theorem

Q59: Use the Guidelines for Graphing Rational Functions

Q60: Use the Guidelines for Graphing Rational Functions

Q61: Use the following to answer questions :<br>y

Q62: Use the following to answer questions :<br>y

Q64: Use Descartes's rule of signs to determine

Q65: Graph the polynomial function.<br>f(x) = x<sup>3</sup> +

Q66: Use the following to answer questions

Q67: Use the Guidelines for Graphing Polynomial Functions

Q68: For the complex polynomial below, one of