Multiple Choice
The range of a projectile is modeled by the function 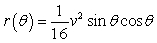 , where v is the initial velocity and is the angle at which the object is initially propelled. The maximum range is achieved when = 45°. Use exact values to compute how many feet short of maximum the projectile falls if = 67.5° and v = 104 ft/sec.
, where v is the initial velocity and is the angle at which the object is initially propelled. The maximum range is achieved when = 45°. Use exact values to compute how many feet short of maximum the projectile falls if = 67.5° and v = 104 ft/sec.
A) 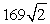 feet
feet
B) 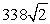 feet
feet
C) 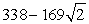 feet
feet
D) 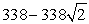 feet
feet
Correct Answer:

Verified
Correct Answer:
Verified
Q87: Find the exact value of the expression
Q88: Use a double-angle identity to find the
Q89: Evaluate without the aid of calculators or
Q90: Verify the equation is an identity using
Q91: Find all solutions in [0, 2π). Answer
Q92: Evaluate. Answer in exact form. <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB3307/.jpg"
Q93: Use the following to answer questions
Q94: Solve the equation in [0, 2π) using
Q96: Use a double-angle identity to find the
Q97: Evaluate. Answer in exact form. <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB3307/.jpg"