Solved

For the Complex Numbers Z1 = 1 - I θ\theta

Question 5

Essay

For the complex numbers z1 = 1 - 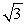For the complex numbers z<sub>1</sub> = 1 - i and z<sub>2</sub> = -5 + 0i (a) Find the moduli r<sub>1</sub> and r<sub>2</sub> and the arguments \theta <sub>1</sub> and \theta <sub>2</sub>. (b) Compute the quotient in rectangular form. (c) Find the modulus r and argument \theta of the quotient. (d) Verify that = r and \theta <sub>1</sub> - \theta <sub>2</sub> = \theta . i and z2 = -5 + 0i
(a) Find the moduli r1 and r2 and the arguments θ\theta 1 and θ\theta 2.
(b) Compute the quotient in rectangular form.
(c) Find the modulus r and argument θ\theta of the quotient.
(d) Verify that For the complex numbers z<sub>1</sub> = 1 - i and z<sub>2</sub> = -5 + 0i (a) Find the moduli r<sub>1</sub> and r<sub>2</sub> and the arguments \theta <sub>1</sub> and \theta <sub>2</sub>. (b) Compute the quotient in rectangular form. (c) Find the modulus r and argument \theta of the quotient. (d) Verify that 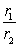= r and \theta <sub>1</sub> - \theta <sub>2</sub> = \theta . = r and θ\theta 1 - θ\theta 2 = θ\theta .

Correct Answer:

verifed

Verified

(a) r1 = 2, r2...

View Answer

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q1: Solve the following equation for a.

Q2: The force vectors F<sub>1</sub> = -5i +

Q3: Determine whether the law of cosines can

Q4: Use the following to answer questions :<br>Vector

Q6: Solve the triangle using the law of

Q7: Use the following to answer questions :<br>u

Q8: Determine whether the law of cosines can

Q9: For the complex numbers z<sub>1</sub> =

Q10: Use the following to answer questions :<br>p

Q11: Use the following to answer questions :