(Continuation of the Purchasing Power Parity Question from Chapter 4)The $\widehat{\text { ActualExRate }}$

Essay

(Continuation of the Purchasing Power Parity question from Chapter 4)The news-magazine The Economist regularly publishes data on the so called Big Mac index and exchange rates between countries. The data for 30 countries from the April 29, 2000 issue is listed below: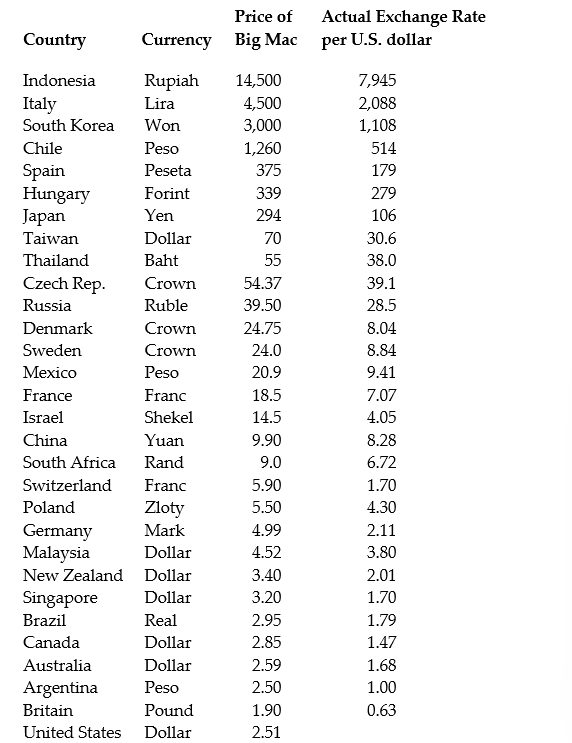

The concept of purchasing power parity or PPP ("the idea that similar foreign and domestic goods … should have the same price in terms of the same currency," Abel, A. and B. Bernanke, Macroeconomics, 4^th edition, Boston: Addison Wesley, 476)suggests that the ratio of the Big Mac priced in the local currency to the U.S. dollar price should equal the exchange rate between the two countries.
After entering the data into your spread sheet program, you calculate the predicted exchange rate per U.S. dollar by dividing the price of a Big Mac in local currency by the U.S. price of a Big Mac ($2.51). To test for PPP, you regress the actual exchange rate on the predicted exchange rate.
The estimated regression is as follows: $\widehat{\text { ActualExRate }}$ = -27.05 + 1.35 × 1.35×Pr edExRate R² = 0.994, n = 29, SER = 122.15
(23.74)(0.02)
(a)Your spreadsheet program does not allow you to calculate heteroskedasticity robust standard errors. Instead, the numbers in parenthesis are homoskedasticity only standard errors. State the two null hypothesis under which PPP holds. Should you use a one-tailed or two-tailed alternative hypothesis?
(b)Calculate the two t-statistics.
(c)Using a 5% significance level, what is your decision regarding the null hypothesis given the two t-statistics? What critical values did you use? Are you concerned with the fact that you are testing the two hypothesis sequentially when they are supposed to hold simultaneously?
(d)What assumptions had to be made for you to use Student's t-distribution?