Solved

If the Underlying Populations Cannot Be Assumed to Be Normal

Question 33

Multiple Choice

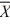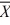If the underlying populations cannot be assumed to be normal, then by the central limit theorem, the sampling distribution of If the underlying populations cannot be assumed to be normal, then by the central limit theorem, the sampling distribution of <sub>1</sub> - <sub>2</sub> is approximately normal only if both sample sizes are sufficiently large-that is, when ________. A) n<sub>1</sub> + n<sub>2</sub> = 30 B) n<sub>1</sub> + n<sub>2</sub> ≥ 30 C) n<sub>1</sub> = 30 and n<sub>2</sub> = 30 D) n<sub>1</sub> ≥ 30 and n<sub>2</sub> ≥ 30 1 - If the underlying populations cannot be assumed to be normal, then by the central limit theorem, the sampling distribution of <sub>1</sub> - <sub>2</sub> is approximately normal only if both sample sizes are sufficiently large-that is, when ________. A) n<sub>1</sub> + n<sub>2</sub> = 30 B) n<sub>1</sub> + n<sub>2</sub> ≥ 30 C) n<sub>1</sub> = 30 and n<sub>2</sub> = 30 D) n<sub>1</sub> ≥ 30 and n<sub>2</sub> ≥ 30 2 is approximately normal only if both sample sizes are sufficiently large-that is, when ________.


A) n1 + n2 = 30
B) n1 + n2 ≥ 30
C) n1 = 30 and n2 = 30
D) n1 ≥ 30 and n2 ≥ 30

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q28: The student senate at a local university

Q29: There is only one type of matched-pairs

Q30: When testing the difference between two population

Q31: The student senate at a local university

Q32: A demographer wants to measure life expectancy

Q34: A tutor promises to improve GMAT scores

Q35: The student senate at a local university

Q36: A student has to decide whether he

Q37: A farmer is concerned that a change

Q38: A new study has found that, on