Solved

The Following Data Show the Demand for an Airline Ticket

Question 26

Multiple Choice

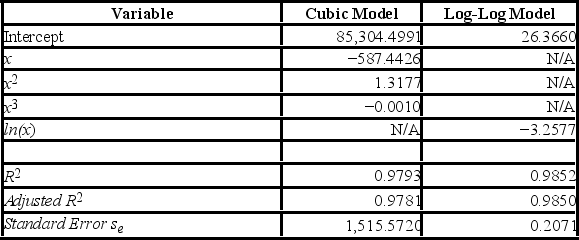The following data show the demand for an airline ticket dependent on the price of this ticket. The following data show the demand for an airline ticket dependent on the price of this ticket. For the assumed cubic and log-log regression models, Demand = β<sub>0</sub> + β<sub>1</sub>Price + β<sub>2</sub>Price<sup>2 </sup>+ β<sub>3</sub>Price<sup>3 </sup>+ ε and ln(Demand) = β<sub>0</sub> + β<sub>1</sub>ln(Price) + ε, the following regression results are available. Which of the following does the slope of the obtained log-log regression equation ln ( ) = 26.3660 - 3.2577 ln(Price) signify? A) For every 1% increase in the price, the predicted demand declines by approximately 3.2577%. B) For every 1% increase in the demand, the expected price increases by approximately 3.2577%. C) For every 1% increase in the demand, the expected price decreases by approximately 3.2577%. D) For every 1% increase in the price, the predicted demand increases by approximately 3.2577%. For the assumed cubic and log-log regression models, Demand = β0 + β1Price + β2Price2 + β3Price3 + ε and ln(Demand) = β0 + β1ln(Price) + ε, the following regression results are available. The following data show the demand for an airline ticket dependent on the price of this ticket. For the assumed cubic and log-log regression models, Demand = β<sub>0</sub> + β<sub>1</sub>Price + β<sub>2</sub>Price<sup>2 </sup>+ β<sub>3</sub>Price<sup>3 </sup>+ ε and ln(Demand) = β<sub>0</sub> + β<sub>1</sub>ln(Price) + ε, the following regression results are available. Which of the following does the slope of the obtained log-log regression equation ln ( ) = 26.3660 - 3.2577 ln(Price) signify? A) For every 1% increase in the price, the predicted demand declines by approximately 3.2577%. B) For every 1% increase in the demand, the expected price increases by approximately 3.2577%. C) For every 1% increase in the demand, the expected price decreases by approximately 3.2577%. D) For every 1% increase in the price, the predicted demand increases by approximately 3.2577%. Which of the following does the slope of the obtained log-log regression equation ln ( The following data show the demand for an airline ticket dependent on the price of this ticket. For the assumed cubic and log-log regression models, Demand = β<sub>0</sub> + β<sub>1</sub>Price + β<sub>2</sub>Price<sup>2 </sup>+ β<sub>3</sub>Price<sup>3 </sup>+ ε and ln(Demand) = β<sub>0</sub> + β<sub>1</sub>ln(Price) + ε, the following regression results are available. Which of the following does the slope of the obtained log-log regression equation ln ( ) = 26.3660 - 3.2577 ln(Price) signify? A) For every 1% increase in the price, the predicted demand declines by approximately 3.2577%. B) For every 1% increase in the demand, the expected price increases by approximately 3.2577%. C) For every 1% increase in the demand, the expected price decreases by approximately 3.2577%. D) For every 1% increase in the price, the predicted demand increases by approximately 3.2577%. ) = 26.3660 - 3.2577 ln(Price) signify?


A) For every 1% increase in the price, the predicted demand declines by approximately 3.2577%.
B) For every 1% increase in the demand, the expected price increases by approximately 3.2577%.
C) For every 1% increase in the demand, the expected price decreases by approximately 3.2577%.
D) For every 1% increase in the price, the predicted demand increases by approximately 3.2577%.

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q21: The quadratic regression model allows for one

Q22: The quadratic regression model <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB6618/.jpg" alt="The

Q23: In which of the following models does

Q24: The fit of the models y =

Q25: A quadratic regression model is a polynomial

Q27: Thirty employed single individuals were randomly selected

Q28: It is believed that the sales volume

Q29: The following data show the cooling temperatures

Q30: The scatterplot shown below represents a typical

Q31: The following data show the cooling temperatures