Multiple Choice
To examine the differences between salaries of male and female middle managers of a large bank, 90 individuals were randomly selected, and two models were created with the following variables considered: Salary = the monthly salary (excluding fringe benefits and bonuses) ,
Educ = the number of years of education,
Exper = the number of months of experience,
Train = the number of weeks of training,
Gender = the gender of an individual; 1 for males, and 0 for females.
Excel partial outputs corresponding to these models are available and shown below.
Model A: Salary = β0 + β1Educ + β2Exper + β3Train + β4Gender + ε 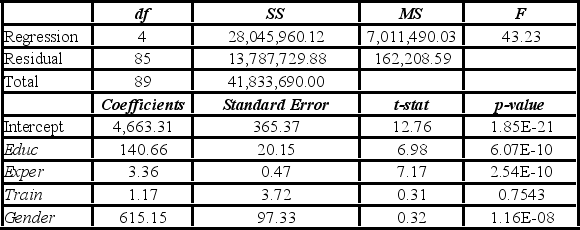 Model B: Salary = β0 + β1Educ + β2Exper + β3Gender + ε
Model B: Salary = β0 + β1Educ + β2Exper + β3Gender + ε 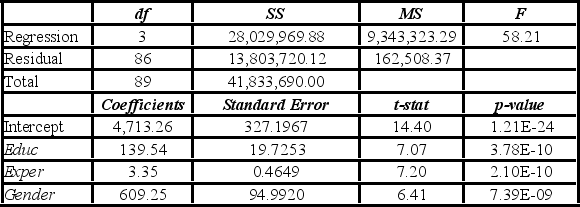 Using Model B, what is the regression equation for males?
Using Model B, what is the regression equation for males?
A) 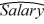 = 4,713.26 + 139.5366Educ + 3.3488Exper + 609.25Gender
= 4,713.26 + 139.5366Educ + 3.3488Exper + 609.25Gender
B) 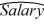 = 5,322.51 + 139.5366Educ + 3.3488Exper
= 5,322.51 + 139.5366Educ + 3.3488Exper
C) 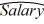 = 4,713.26 + 139.5366Educ + 3.3488Exper
= 4,713.26 + 139.5366Educ + 3.3488Exper
D) 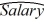 = 4,663.31 + 140.6634Educ + 3.3566Exper
= 4,663.31 + 140.6634Educ + 3.3566Exper
Correct Answer:

Verified
Correct Answer:
Verified
Q102: According to the Center for Disease Control
Q103: A researcher wants to examine how the
Q104: For the model y = β<sub>0 </sub>+
Q105: Like any other university, Seton Hall University
Q106: According to the Center for Disease Control
Q108: A bank manager is interested in assigning
Q109: A realtor wants to predict and compare
Q110: A researcher wants to examine how the
Q111: Variables employed in a regression model can
Q112: An over-the-counter drug manufacturer wants to examine