To Examine the Differences Between Salaries of Male and Female

Multiple Choice

To examine the differences between salaries of male and female middle managers of a large bank, 90 individuals were randomly selected, and two models were created with the following variables considered: Salary = the monthly salary (excluding fringe benefits and bonuses) ,
Educ = the number of years of education,
Exper = the number of months of experience,
Train = the number of weeks of training,
Gender = the gender of an individual; 1 for males, and 0 for females.
The Excel partial outputs corresponding to these models are available and shown below.
Model A: Salary = β₀ + β₁Educ + β₂Exper + β₃Train + β₄Gender + ε Model B: Salary = β₀ + β₁Educ + β₂Exper + β₃Gender + ε 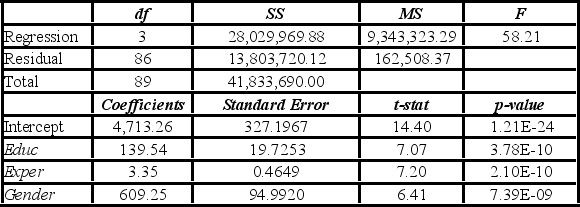A group of female managers considers a discrimination lawsuit if on average their salaries could be statistically proven to be lower by more than $500 than the salaries of their male peers with the same level of education and experience. Using Model B, what is the conclusion of the appropriate test at 10% significance level?

A) Do not reject H₀; the salaries of female managers cannot be proven to be lower on average by more than $500.
B) Reject H₀; the salaries of female managers cannot be proven to be lower on average by more than $500.
C) Do not reject H₀; the salaries of female managers are lower on average by more than $500.
D) Reject H₀; the salaries of female managers are lower on average by more than $500.