Instruction 12 $\text { Regression statistics }$ $\text { ANOVA }$

True/False

Instruction 12.26
The manager of the purchasing department of a large savings and loan organization would like to develop a model to predict the amount of time (measured in hours) it takes to record a loan application. Data are collected from a sample of 30 days, and the number of applications recorded and completion time in hours is recorded. Below is the regression output:
$\text { Regression statistics }$
$\begin{array}{|l|l|}\hline\text { MultipleR } & 0.9447 \\\hline \text { R Square } & 0.8924 \\\hline \begin{array}{l}\text { Adjusted R } \\\text { Square }\end{array} & 0.8886 \\\hline \text { Standard Error } & 0.3342 \\\hline \text { Observations } & 30 \\\hline\end{array}$

$\text { ANOVA }$
$\begin{array}{|l|l|l|l|l|l|}\hline & d f & S 5 & M S & F & \begin{array}{l}\text { Significance } \\F\end{array} \\\hline \text { Regression } & 1 & 25.9438 & 25.9438 & 232.2200 & 4.3946 \mathrm{E}-15 \\\hline \text { Residual } & 28 & 3.1282 & 0.1117 & & \\\hline \text { Total } & 29 & 29.072 & & & \\\hline\end{array}$

$\begin{array}{|l|l|l|l|l|l|l|}\hline & \text { Coefficients } & \begin{array}{l}\text { Standard } \\\text { Error }\end{array} & \text { tStat } & \text { p-value } & \text { Lower 95\% } & \text { Upper 95\% } \\\hline \text { Intercept } & 0.4024 & 0.1236 & 3.2559 & 0.0030 & 0.1492 & 0.6555 \\\hline \begin{array}{l}\text { Applications } \\\text { Recorded }\end{array} & 0.0126 & 0.0008 & 15.2388 & \begin{array}{l}4.3946 \mathrm{E}- \\15\end{array} & 0.0109 & 0.0143 \\\hline\end{array}$



Note: 4.3946E-15 is 4.3946 × 10^-15.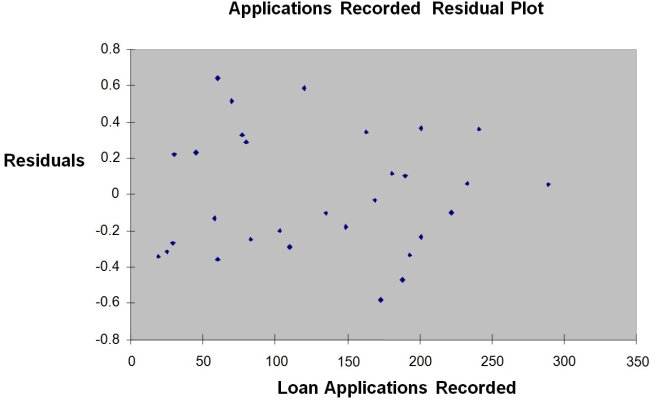
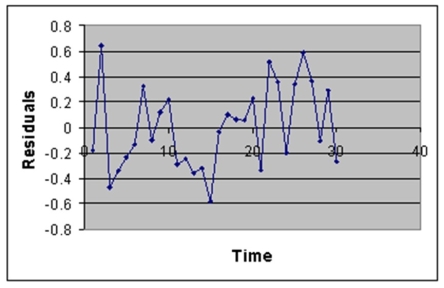
-Referring to Instruction 12.26,there is no evidence of positive autocorrelation if the Durbin-Watson test statistic is found to be 1.78.