Solved

The Angle Between Vector = 2

Question 66

Multiple Choice

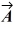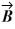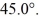The angle between vector The angle between vector = 2.00 + 3.00 and vector is The scalar product of vectors and is 3.00.If the x component of vector is positive,what is vector . A) B) C) D) E) = 2.00 The angle between vector = 2.00 + 3.00 and vector is The scalar product of vectors and is 3.00.If the x component of vector is positive,what is vector . A) B) C) D) E) + 3.00 The angle between vector = 2.00 + 3.00 and vector is The scalar product of vectors and is 3.00.If the x component of vector is positive,what is vector . A) B) C) D) E) and vector The angle between vector = 2.00 + 3.00 and vector is The scalar product of vectors and is 3.00.If the x component of vector is positive,what is vector . A) B) C) D) E) is The angle between vector = 2.00 + 3.00 and vector is The scalar product of vectors and is 3.00.If the x component of vector is positive,what is vector . A) B) C) D) E) The scalar product of vectors The angle between vector = 2.00 + 3.00 and vector is The scalar product of vectors and is 3.00.If the x component of vector is positive,what is vector . A) B) C) D) E) and The angle between vector = 2.00 + 3.00 and vector is The scalar product of vectors and is 3.00.If the x component of vector is positive,what is vector . A) B) C) D) E) is 3.00.If the x component of vector The angle between vector = 2.00 + 3.00 and vector is The scalar product of vectors and is 3.00.If the x component of vector is positive,what is vector . A) B) C) D) E) is positive,what is vector The angle between vector = 2.00 + 3.00 and vector is The scalar product of vectors and is 3.00.If the x component of vector is positive,what is vector . A) B) C) D) E) .


A) The angle between vector = 2.00 + 3.00 and vector is The scalar product of vectors and is 3.00.If the x component of vector is positive,what is vector . A) B) C) D) E)
B) The angle between vector = 2.00 + 3.00 and vector is The scalar product of vectors and is 3.00.If the x component of vector is positive,what is vector . A) B) C) D) E)
C) The angle between vector = 2.00 + 3.00 and vector is The scalar product of vectors and is 3.00.If the x component of vector is positive,what is vector . A) B) C) D) E)
D) The angle between vector = 2.00 + 3.00 and vector is The scalar product of vectors and is 3.00.If the x component of vector is positive,what is vector . A) B) C) D) E)
E) The angle between vector = 2.00 + 3.00 and vector is The scalar product of vectors and 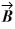is 3.00.If the x component of vector 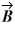is positive,what is vector . A) 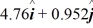B) 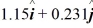C) 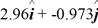D) 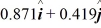E)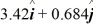

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q61: If <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB6394/.jpg" alt="If =

Q62: The current definition of the standard kilogram

Q63: The magnitude of a vector can never

Q64: In the figure,the magnitude of vector <img

Q65: Vector <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB6394/.jpg" alt="Vector has

Q67: An apple falls from an apple tree

Q68: If a flower is 6.5 cm wide,its

Q69: Three forces are exerted on an object

Q70: The exhaust fan on a typical kitchen

Q71: A helicopter is flying horizontally with a