Solved

Consider the Following Linear Program

Question 43

Essay

Consider the following linear program:
MAX 3x1 + 4x2 ($ Profit)
s.t.x1 + 3x2 < 12
2x1 + x2 < 8
x1 < 3
x1,x2 > 0
The Management Scientist provided the following solution output:
OPTIMAL SOLUTION
Objective Function Value = 20.000
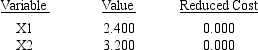
Consider the following linear program: MAX 3x<sub>1</sub> + 4x<sub>2</sub> ($ Profit) s.t.x<sub>1</sub> + 3x<sub>2</sub> < 12 2x<sub>1</sub> + x<sub>2</sub> < 8 x<sub>1</sub> < 3 x<sub>1</sub>,x<sub>2 </sub> > 0 The Management Scientist provided the following solution output: OPTIMAL SOLUTION Objective Function Value = 20.000 OBJECTIVE COEFFICIENT RANGES RIGHT HAND SIDE RANGES a.What is the optimal solution including the optimal value of the objective function? b.Suppose the profit on x<sub>1</sub> is increased to $7.Is the above solution still optimal? What is the value of the objective function when this unit profit is increased to $7? c.If the unit profit on x<sub>2</sub> was $10 instead of $4,would the optimal solution change? d.If simultaneously the profit on x<sub>1</sub> was raised to $5.5 and the profit on x<sub>2</sub> was reduced to $3,would the current solution still remain optimal? Consider the following linear program: MAX 3x<sub>1</sub> + 4x<sub>2</sub> ($ Profit) s.t.x<sub>1</sub> + 3x<sub>2</sub> < 12 2x<sub>1</sub> + x<sub>2</sub> < 8 x<sub>1</sub> < 3 x<sub>1</sub>,x<sub>2 </sub> > 0 The Management Scientist provided the following solution output: OPTIMAL SOLUTION Objective Function Value = 20.000 OBJECTIVE COEFFICIENT RANGES RIGHT HAND SIDE RANGES a.What is the optimal solution including the optimal value of the objective function? b.Suppose the profit on x<sub>1</sub> is increased to $7.Is the above solution still optimal? What is the value of the objective function when this unit profit is increased to $7? c.If the unit profit on x<sub>2</sub> was $10 instead of $4,would the optimal solution change? d.If simultaneously the profit on x<sub>1</sub> was raised to $5.5 and the profit on x<sub>2</sub> was reduced to $3,would the current solution still remain optimal? OBJECTIVE COEFFICIENT RANGES
Consider the following linear program: MAX 3x<sub>1</sub> + 4x<sub>2</sub> ($ Profit) s.t.x<sub>1</sub> + 3x<sub>2</sub> < 12 2x<sub>1</sub> + x<sub>2</sub> < 8 x<sub>1</sub> < 3 x<sub>1</sub>,x<sub>2 </sub> > 0 The Management Scientist provided the following solution output: OPTIMAL SOLUTION Objective Function Value = 20.000 OBJECTIVE COEFFICIENT RANGES RIGHT HAND SIDE RANGES a.What is the optimal solution including the optimal value of the objective function? b.Suppose the profit on x<sub>1</sub> is increased to $7.Is the above solution still optimal? What is the value of the objective function when this unit profit is increased to $7? c.If the unit profit on x<sub>2</sub> was $10 instead of $4,would the optimal solution change? d.If simultaneously the profit on x<sub>1</sub> was raised to $5.5 and the profit on x<sub>2</sub> was reduced to $3,would the current solution still remain optimal? RIGHT HAND SIDE RANGES
Consider the following linear program: MAX 3x<sub>1</sub> + 4x<sub>2</sub> ($ Profit) s.t.x<sub>1</sub> + 3x<sub>2</sub> < 12 2x<sub>1</sub> + x<sub>2</sub> < 8 x<sub>1</sub> < 3 x<sub>1</sub>,x<sub>2 </sub> > 0 The Management Scientist provided the following solution output: OPTIMAL SOLUTION Objective Function Value = 20.000 OBJECTIVE COEFFICIENT RANGES RIGHT HAND SIDE RANGES a.What is the optimal solution including the optimal value of the objective function? b.Suppose the profit on x<sub>1</sub> is increased to $7.Is the above solution still optimal? What is the value of the objective function when this unit profit is increased to $7? c.If the unit profit on x<sub>2</sub> was $10 instead of $4,would the optimal solution change? d.If simultaneously the profit on x<sub>1</sub> was raised to $5.5 and the profit on x<sub>2</sub> was reduced to $3,would the current solution still remain optimal?
a.What is the optimal solution including the optimal value of the objective function?
b.Suppose the profit on x1 is increased to $7.Is the above solution still optimal? What is the value of the objective function when this unit profit is increased to $7?
c.If the unit profit on x2 was $10 instead of $4,would the optimal solution change?
d.If simultaneously the profit on x1 was raised to $5.5 and the profit on x2 was reduced to $3,would the current solution still remain optimal?

Correct Answer:

verifed

Verified

a.x1 = 2.4 and x2 = 3.2,and z = $20.00.
b....

View Answer

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q11: For any constraint, either its slack/surplus value

Q20: When the cost of a resource is

Q21: In a linear programming problem,the binding constraints

Q24: A constraint with a positive slack value<br>A)will

Q29: If the dual price for the right-hand

Q31: Which of the following is not a

Q41: Consider the following linear program:<br>MIN 6x<sub>1</sub> +

Q43: The dual price measures, per unit increase

Q44: There is a dual price for every

Q47: The binding constraints for this problem