Short Answer
An open box is formed by cutting a square piece out of each corner of a 8-inch by 12-inch piece of metal.If each side of the squares cut out is x inches long,the volume of the box is given by 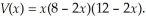
This problem only makes sense when this volume is positive.Find the values of x for which the volume is positive.
Correct Answer:

Verified
Correct Answer:
Verified
Q41: The volume of helium in a spherical
Q42: The length of a material increases as
Q43: Solve: <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB6578/.jpg" alt="Solve:
Q44: The solution of (x + 1)( <img
Q45: The solution of <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB6578/.jpg" alt="The solution
Q47: Find: Find <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB6578/.jpg" alt="Find: Find
Q48: The solution of <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB6578/.jpg" alt="The solution
Q49: Let f(x)= <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB6578/.jpg" alt="Let f(x)=
Q50: Find the following limit.If it is +∞
Q51: Find the following limit.If it is +∞