Essay
Determine the intervals on which the function is increasing and on which it is decreasing.Also determine the points of relative maxima and relative minima.
f(x)= ( 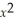
- 3x + 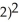
Correct Answer:

Verified
Increasing on the intervals  _T...
_T...View Answer
Unlock this answer now
Get Access to more Verified Answers free of charge
Correct Answer:
Verified
View Answer
Unlock this answer now
Get Access to more Verified Answers free of charge
Q105: Find all the critical values of f(x)=
Q106: A released film has a revenue given
Q107: The function y = <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB6578/.jpg" alt="The
Q108: Find all the critical values of f(x)=
Q109: The function f(x)= 4 <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB6578/.jpg" alt="The
Q111: Find two numbers whose sum is 30
Q112: On the interval <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB6578/.jpg" alt="On the
Q113: Let y = 3 <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB6578/.jpg" alt="Let
Q114: Find the intervals where the graph of
Q115: A rectangular plot adjacent to a stream