Essay
Determine the intervals on which the function is increasing and on which it is decreasing.Also determine the points of relative maxima and relative minima.
y = 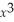
+ 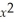
- 3x + 7
Correct Answer:

Verified
Increasing on the intervals  _T...
_T...View Answer
Unlock this answer now
Get Access to more Verified Answers free of charge
Correct Answer:
Verified
View Answer
Unlock this answer now
Get Access to more Verified Answers free of charge
Q137: Determine the equations of the vertical asymptotes
Q138: Let f(x)= <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB6578/.jpg" alt="Let f(x)=
Q139: Find the intervals where the graph of
Q140: If f(x)= <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB6578/.jpg" alt="If f(x)=
Q141: Find the vertical asymptotes and non-vertical asymptotes
Q143: Given y = f(x)= 4 <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB6578/.jpg"
Q144: The cost equation for a cookie store
Q145: The graph of a function is given.Find<br>(a)the
Q146: Let f(x)= <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB6578/.jpg" alt="Let f(x)=
Q147: Find all the critical values of y