Essay
The random variable X has the cumulative distribution function F(x)whose value or derivative 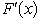 is shown below for various values of x.F(0)= 0,
is shown below for various values of x.F(0)= 0, 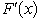 =
= 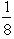 ,for 0 < x < 2,P(X = 2)=
,for 0 < x < 2,P(X = 2)= 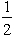 ,so F(2)=
,so F(2)= 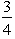 ,
, 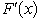 =
= 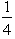 ,for 2 < x < 3,F(3)= 1.Generate four random observations from this probability distribution by using the following uniform random numbers:
,for 2 < x < 3,F(3)= 1.Generate four random observations from this probability distribution by using the following uniform random numbers: 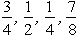 .Also calculate the sample average and compare it with the true mean
.Also calculate the sample average and compare it with the true mean 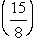 for this probability distribution.
for this probability distribution.
Correct Answer:

Verified
Correct Answer:
Verified
Related Questions