Solved

The Repeating Decimal Is Expressed as a Geometric Series

Question 81

Multiple Choice

The repeating decimal The repeating decimal is expressed as a geometric series Write the decimal as the ratio of two integers. ​​ A) ​ B) ​ C) ​ D) ​ E) ​ is expressed as a geometric series The repeating decimal is expressed as a geometric series Write the decimal as the ratio of two integers. ​​ A) ​ B) ​ C) ​ D) ​ E) ​ Write the decimal The repeating decimal is expressed as a geometric series Write the decimal as the ratio of two integers. ​​ A) ​ B) ​ C) ​ D) ​ E) ​ as the ratio of two integers. ​​


A) ​ The repeating decimal is expressed as a geometric series Write the decimal as the ratio of two integers. ​​ A) ​ B) ​ C) ​ D) ​ E) ​
B) ​ The repeating decimal is expressed as a geometric series Write the decimal as the ratio of two integers. ​​ A) ​ B) ​ C) ​ D) ​ E) ​
C) ​ The repeating decimal is expressed as a geometric series Write the decimal as the ratio of two integers. ​​ A) ​ B) ​ C) ​ D) ​ E) ​
D) The repeating decimal is expressed as a geometric series Write the decimal as the ratio of two integers. ​​ A) ​ B) ​ C) ​ D) ​ E) ​ ​
E) ​ The repeating decimal is expressed as a geometric series Write the decimal 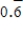as the ratio of two integers. ​​ A) ​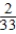 B) ​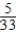 C) ​ D) ​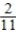 E) ​

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q76: ​Find the sum of the convergent series.

Q77: ​Determine the convergence or divergence of the

Q78: Find the limit of the following sequence.

Q79: ​Use Newton´s Method to approximate the zero(s)of

Q80: ​Use Newton´s Method to approximate the zero(s)of

Q82: The value for which Newton's method fails

Q83: ​Determine the convergence or divergence of the

Q84: ​Apply Taylor's Theorem to find the power

Q85: ​Bouncing Ball.A ball dropped from a height

Q86: Find the limit of the following sequence.