Solved

The (Inverse) Demand in a Cournot Duopoly Is P =

Question 92

Essay

The (inverse) demand in a Cournot duopoly is P = a - b (Q1 + Q2), and costs are C1(Q1) = c1Q1 and C2(Q2) = c2Q2. Show that the Cournot equilibrium levels of output are The (inverse) demand in a Cournot duopoly is P = a - b (Q<sub>1</sub> + Q<sub>2</sub>), and costs are C<sub>1</sub>(Q<sub>1</sub>) = c<sub>1</sub>Q<sub>1</sub> and C<sub>2</sub>(Q<sub>2</sub>) = c<sub>2</sub>Q<sub>2</sub>. Show that the Cournot equilibrium levels of output are 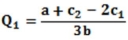and . and The (inverse) demand in a Cournot duopoly is P = a - b (Q<sub>1</sub> + Q<sub>2</sub>), and costs are C<sub>1</sub>(Q<sub>1</sub>) = c<sub>1</sub>Q<sub>1</sub> and C<sub>2</sub>(Q<sub>2</sub>) = c<sub>2</sub>Q<sub>2</sub>. Show that the Cournot equilibrium levels of output are and . .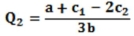

Correct Answer:

verifed

Verified

Equating MR = MC for firm 1 yields a - b...

View Answer

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q14: The Bertrand model of oligopoly reveals that:<br>A)

Q47: Both firms in a Cournot duopoly would

Q52: Collusion in oligopoly is difficult to achieve

Q80: Consider two firms competing to sell a

Q88: Which of the following is true?<br>A) If

Q93: An increase in firm 2's marginal cost

Q97: Consider a Stackelberg duopoly with the following

Q111: Which of the following is NOT a

Q118: Consider a market consisting of two firms

Q130: If firms are in Cournot equilibrium:<br>A) each