Instruction 12-12
the Manager of the Purchasing Department of a Large

Multiple Choice

Instruction 12-12
The manager of the purchasing department of a large savings and loan organization would like to develop a model to predict the amount of time (measured in hours) it takes to record a loan application.Data are collected from a sample of 30 days,and the number of applications recorded and completion time in hours is recorded.Below is the regression output:
$$\begin{array}{l}\begin{array} { l r } \hline { \text { Regression Statistics } } \\\hline \text { Multiple R } & 0.9447 \\\text { R Square } & 0.8924 \\\text { Adjusted R } & 0.8886 \\\text { Square } & \\\text { Standard } & 0.3342 \\\text { Error } & 30 \\\text { Observations } & \\\hline\end{array}\\\text { ANOVA }\\\begin{array} { l r r r r r } \hline & d f & { \text { SS } } & { \text { MS } } & F & { \begin{array} { c } \text { Significance } \\F\end{array} } \\\hline \text { Regression } & 1 & 25.9438 & 25.9438 & 232.2200 & 4.3946 \mathrm { E } - 15 \\\text { Residual } & 28 & 3.1282 & 0.1117 & & \\\text { Total } & 29 & 29.072 & & & \\\hline\end{array}\\\begin{array} { l r r r r r r } \hline & \text { Coefficients } & \begin{array} { c } \text { Standard } \\\text { Error }\end{array} & t \text { Stat } & P \text {-value } & \text { Lower 95\% } & \text { Upper 95\% } \\\hline \begin{array} { l } \text { Intercept } \\\text { Applications } \\\text { Recorded }\end{array} & 0.4024 & 0.1236 & 3.2559 & 0.0030 & 0.1492 & 0.6555 \\\hline\end{array}\end{array}$$ Note: 4.3946E-15 is 4.3946 x 10^-15.

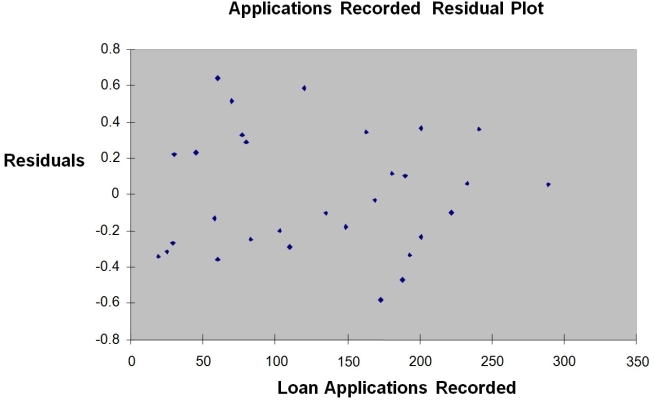
-Referring to Instruction 12-12,the error sum of squares (SSE) of the above regression is

A) 0.1117.
B) 29.0720.
C) 25.9438.
D) 3.1282.