Essay
Doctors studying how the human body assimilates medication inject some patients with penicillin,and then monitor the concentration of the drug (in units/cc)in the patients' blood for seven hours.First they tried to fit a linear model.The regression analysis and residuals plot are shown.Is that estimate likely to be accurate,too low,or too high? Explain. Dependent variable is: Concentration
No Selector
R squared R squared (adjusted)
with degrees of freedom
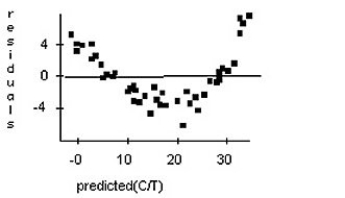
Correct Answer:

Verified
Too high; the residu...View Answer
Unlock this answer now
Get Access to more Verified Answers free of charge
Correct Answer:
Verified
View Answer
Unlock this answer now
Get Access to more Verified Answers free of charge
Q52: A golf ball is dropped from
Q53: The relationship between the number of
Q54: <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB3450/.jpg" alt=" A)Model is appropriate.
Q55: The relationship between the number of
Q56: If the linear correlation between shoe size
Q58: The relationship between the number of
Q59: A golf ball is dropped from
Q60: A random sample of 150 yachts
Q61: Using advertised prices for used Ford
Q62: Ten Ford Escort classified ads were