Multiple Choice
Below is a graph of function f(x) . Which of the following could be the second Taylor polynomial of f(x) at 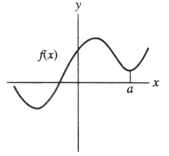
A) (x) = + (x - a)
B) (x) = +
C) (x) = -
D) (x) = - (x - a) +
E) (x) = (x - a) -
Correct Answer:

Verified
Correct Answer:
Verified
Related Questions
Q87: Find the second Taylor polynomial of
Q88: Let <span class="ql-formula" data-value="x _0"><span
Q89: Determine the sum of the following
Q90: Use the comparison test to determine
Q91: Find the Taylor Series at x
Q93: Use the integral test to determine
Q94: Below is a graph of the
Q95: Determine the third Taylor polynomial of
Q96: Determine the first three non-zero terms
Q97: Determine the sum of the series