Solved

Three Balls Are Drawn, Without Replacement, from a Bag Containing

Question 164

Multiple Choice

Three balls are drawn, without replacement, from a bag containing 9 red balls and 4 white balls. Construct a probability tree to determine the probability that three white W balls are drawn. ​


A) Pr(three W) = Three balls are drawn, without replacement, from a bag containing 9 red balls and 4 white balls. Construct a probability tree to determine the probability that three white W balls are drawn. ​ A) Pr(three W) = B) Pr(three W) = C) Pr(three W) = D) Pr(three W) = E) Pr(three W) =
B) Pr(three W) = Three balls are drawn, without replacement, from a bag containing 9 red balls and 4 white balls. Construct a probability tree to determine the probability that three white W balls are drawn. ​ A) Pr(three W) = B) Pr(three W) = C) Pr(three W) = D) Pr(three W) = E) Pr(three W) =
C) Pr(three W) = Three balls are drawn, without replacement, from a bag containing 9 red balls and 4 white balls. Construct a probability tree to determine the probability that three white W balls are drawn. ​ A) Pr(three W) = B) Pr(three W) = C) Pr(three W) = D) Pr(three W) = E) Pr(three W) =
D) Pr(three W) = Three balls are drawn, without replacement, from a bag containing 9 red balls and 4 white balls. Construct a probability tree to determine the probability that three white W balls are drawn. ​ A) Pr(three W) = B) Pr(three W) = C) Pr(three W) = D) Pr(three W) = E) Pr(three W) =
E) Pr(three W) = Three balls are drawn, without replacement, from a bag containing 9 red balls and 4 white balls. Construct a probability tree to determine the probability that three white W balls are drawn. ​ A) Pr(three W) = 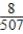B) Pr(three W) = 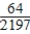C) Pr(three W) = 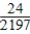D) Pr(three W) = 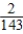E) Pr(three W) =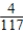

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q38: A game of cards is played with

Q84: Assuming there are 365 different birthdays, find

Q99: Five percent of the population of the

Q160: A box contains 3 red balls, 5

Q161: A ball is drawn from a bag

Q164: Suppose that all license plates in a

Q165: A bag contains 9 white balls W

Q166: If the probability that an event will

Q167: A red ball and 18 white balls

Q169: An automatic teller machine requires that each