Multiple Choice
In a certain city, the Democratic, Republican, and Consumer parties have members of their parties on the city council. The probability of a member of this party winning in any election depends on the proportional membership of his/her party at the time of the election. The probabilities for all these parties winning are given by the following transition matrix P. Using the given transition matrix and assuming the initial-probability vector is 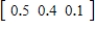 , find the probability vectors for the next four steps of the Markov chain. Round all numerical values in your answer to four decimal places.
, find the probability vectors for the next four steps of the Markov chain. Round all numerical values in your answer to four decimal places. 
A) 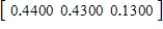 ,
, 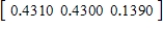 ,
, 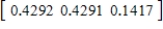 ,
, 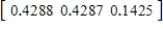
B)  ,
, 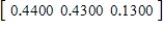 ,
, 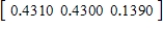 ,
, 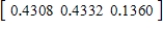
C) 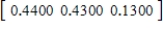 ,
, 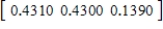 ,
, 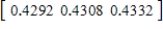 ,
, 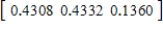
D) 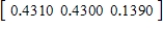 ,
,  ,
, 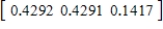 ,
, 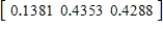
E) 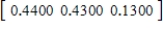 ,
, 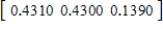 ,
, 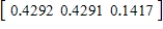 ,
, 
Correct Answer:

Verified
Correct Answer:
Verified
Q43: A small town has 8000 adult males
Q44: A small town has 5000 adult males
Q97: A bag contains 5 white balls and
Q98: Can the matrix <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB4005/.jpg" alt="Can the
Q98: Each computer component that the Peggos Company
Q100: On June 16, 1997, two amateur golfers
Q101: If you draw one card at random
Q103: Each of urns I and II has
Q105: Three balls are drawn, without replacement, from
Q106: A bag contains 5 white balls and