Multiple Choice
A company has the Cobb-Douglas production function 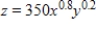 , where x is the number of units of labor, y is the number of units of capital, and z is the units of production. Suppose labor costs $200 per unit, capital costs $150 per unit, and the total cost of labor and capital is limited to $300,000. Find the number of units of labor and the number of units of capital that maximize production.
, where x is the number of units of labor, y is the number of units of capital, and z is the units of production. Suppose labor costs $200 per unit, capital costs $150 per unit, and the total cost of labor and capital is limited to $300,000. Find the number of units of labor and the number of units of capital that maximize production.
A) 1,500 units of labor; 2,000 units of capital
B) 1,200 units of labor; 2,000 units of capital
C) 1,500 units of labor; 400 units of capital
D) 1,200 units of labor; 400 units of capital
E) 12,000 units of labor; 4,000 units of capital
Correct Answer:

Verified
Correct Answer:
Verified
Q66: Find x and y such that <img
Q67: If <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB4005/.jpg" alt="If ,
Q68: Find the dimensions (in centimeters) of the
Q69: Find the values for each of the
Q70: Test <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB4005/.jpg" alt="Test for
Q72: Find the slope of the tangent in
Q73: On the basis of past experience, a
Q74: If <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB4005/.jpg" alt="If ,
Q75: Suppose that an indifference curve for two
Q76: Test for relative maximum and minimum.