Solved

When the Area Under from to Is

Question 171

Multiple Choice

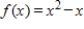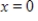When the area under When the area under from to is approximated, the formulas for the sum of n rectangles using left-hand endpoints and right-hand endpoints are: ​ Left-hand endpoints: ​ Right-hand endpoints: ​ Find ​ A) ​ ​ B) ​ ​ C) ​ ​ D) ​ ​ E) ​ ​ from When the area under from to is approximated, the formulas for the sum of n rectangles using left-hand endpoints and right-hand endpoints are: ​ Left-hand endpoints: ​ Right-hand endpoints: ​ Find ​ A) ​ ​ B) ​ ​ C) ​ ​ D) ​ ​ E) ​ ​ to When the area under from to is approximated, the formulas for the sum of n rectangles using left-hand endpoints and right-hand endpoints are: ​ Left-hand endpoints: ​ Right-hand endpoints: ​ Find ​ A) ​ ​ B) ​ ​ C) ​ ​ D) ​ ​ E) ​ ​ is approximated, the formulas for the sum of n rectangles using left-hand endpoints and right-hand endpoints are: ​
Left-hand endpoints: When the area under from to is approximated, the formulas for the sum of n rectangles using left-hand endpoints and right-hand endpoints are: ​ Left-hand endpoints: ​ Right-hand endpoints: ​ Find ​ A) ​ ​ B) ​ ​ C) ​ ​ D) ​ ​ E) ​ ​ ​
Right-hand endpoints: When the area under from to is approximated, the formulas for the sum of n rectangles using left-hand endpoints and right-hand endpoints are: ​ Left-hand endpoints: ​ Right-hand endpoints: ​ Find ​ A) ​ ​ B) ​ ​ C) ​ ​ D) ​ ​ E) ​ ​ ​
Find When the area under from to is approximated, the formulas for the sum of n rectangles using left-hand endpoints and right-hand endpoints are: ​ Left-hand endpoints: ​ Right-hand endpoints: ​ Find ​ A) ​ ​ B) ​ ​ C) ​ ​ D) ​ ​ E) ​ ​ ​


A) ​ When the area under from to is approximated, the formulas for the sum of n rectangles using left-hand endpoints and right-hand endpoints are: ​ Left-hand endpoints: ​ Right-hand endpoints: ​ Find ​ A) ​ ​ B) ​ ​ C) ​ ​ D) ​ ​ E) ​ ​
​
B) ​ When the area under from to is approximated, the formulas for the sum of n rectangles using left-hand endpoints and right-hand endpoints are: ​ Left-hand endpoints: ​ Right-hand endpoints: ​ Find ​ A) ​ ​ B) ​ ​ C) ​ ​ D) ​ ​ E) ​ ​
​
C) ​ When the area under from to is approximated, the formulas for the sum of n rectangles using left-hand endpoints and right-hand endpoints are: ​ Left-hand endpoints: ​ Right-hand endpoints: ​ Find ​ A) ​ ​ B) ​ ​ C) ​ ​ D) ​ ​ E) ​ ​
​
D) ​ When the area under from to is approximated, the formulas for the sum of n rectangles using left-hand endpoints and right-hand endpoints are: ​ Left-hand endpoints: ​ Right-hand endpoints: ​ Find ​ A) ​ ​ B) ​ ​ C) ​ ​ D) ​ ​ E) ​ ​
​
E) ​ When the area under from to 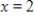is approximated, the formulas for the sum of n rectangles using left-hand endpoints and right-hand endpoints are: ​ Left-hand endpoints: ​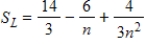 Right-hand endpoints: ​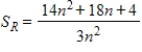 Find ​ A) ​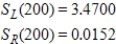 ​ B) ​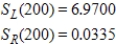 ​ C) ​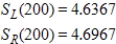 ​ D) ​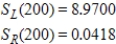 ​ E) ​ ​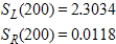
​

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q40: Suppose that the rate of production of

Q166: Suppose that a vending machine company is

Q168: Find the value of the sum <img

Q169: Approximate the area under the curve over

Q170: If the supply function for x units

Q172: The demand function for a product is

Q173: Determine the most appropriate method or integral

Q174: Suppose spending for a wireless communications services

Q175: Evaluate the definite integral <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB4005/.jpg" alt="Evaluate

Q176: Evaluate the integral <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB4005/.jpg" alt="Evaluate the