Suppose That the Rate at Which a Nuclear Power Plant

Multiple Choice

Suppose that the rate at which a nuclear power plant produces radioactive waste is proportional to the number of years it has been operating, according to 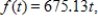in pounds per year. Suppose also that the waste decays exponentially at a rate of 6% per year. Then the amount of radioactive waste that will accumulate in b years is given by 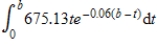and this integral evaluates to 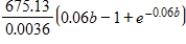. How much waste will accumulate in the long run? Take the limit as 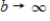in the integral evaluated. Round your answer to the nearest pound, if it exists. ​

A) Approximately 187,536 pounds of waste will accumulate in the long run.
B) Approximately 11,252 pounds of waste will accumulate in the long run.
C) Approximately 176,284 pounds of waste will accumulate in the long run.
D) 0 (No waste will accumulate in the long run.)
E) (Waste is produced more rapidly than existing waste decays.)