Multiple Choice
A person plans to invest up to $26,000 in two different interest-bearing accounts.Each account is to contain at least $5000.Moreover,the amount in one account should be at least twice the amount in the other account.Find and graph a system of inequalities to describe the various amounts that can be deposited in each account.
A) 
B) 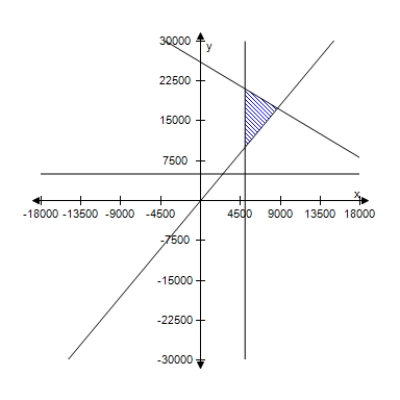
C) 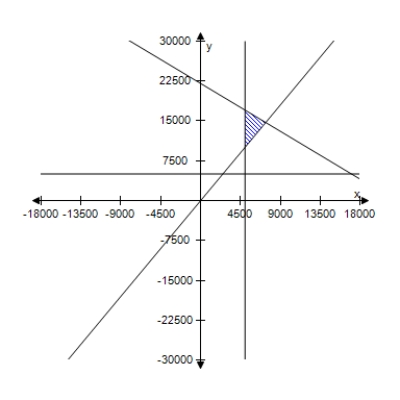
D) 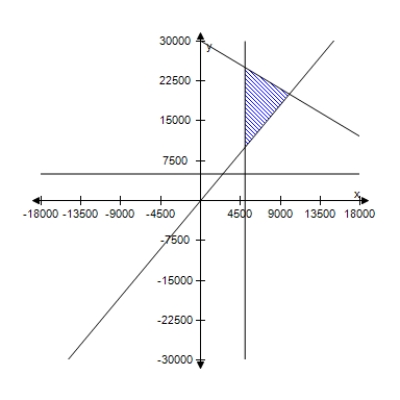
E) 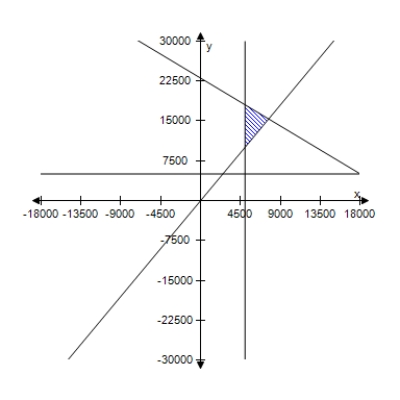
Correct Answer:

Verified
Correct Answer:
Verified
Q19: Select the correct graph of the
Q20: A dietitian is asked to design
Q21: Select the correct graph of the
Q22: Derive a set of inequalities to
Q23: Select an inequality for the shaded
Q25: Select the correct graph of the
Q26: Find the consumer surplus and producer
Q27: Select an inequality to describe the
Q28: Sketch the graph of the inequality.
Q29: Select a set of inequalities to