Use a Graphing Utility to Select the Graph of the Two

Multiple Choice

Use a graphing utility to select the graph of the two equations in the same viewing window.Use the graphs to determine whether the expressions are equivalent.​ $\begin{array} { l } y _ { 1 } = 2 \sin x \csc x , \\y _ { 2 } = 2\end{array}$ ​

A) ​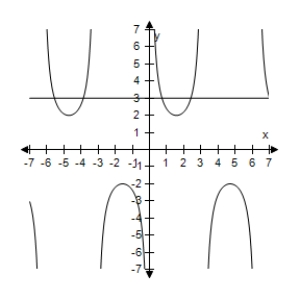 The expressions are equivalent except
Sinx = 0,y₁ is undefined.
B) ​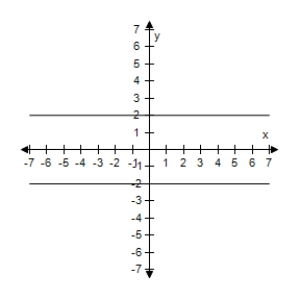 The expressions are equivalent except when sinx = 0,y₁ is undefined.
C) ​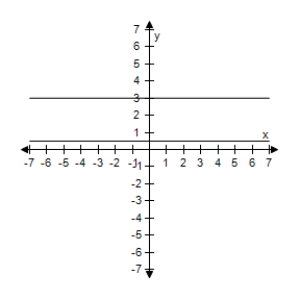 The expressions are equivalent except when
Sinx = 0,y₁ is undefined.
D) ​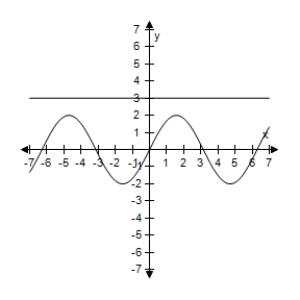 The expressions are equivalent except when sinx = 0,y₁ is undefined.
E) ​ The expressions are equivalent except when sinx = 0,y₁ is undefined.