Multiple Choice
Use the change-of-base formula to rewrite the logarithm as a ratio of logarithms.Then use a graphing utility to graph the ratio.? ?
A) 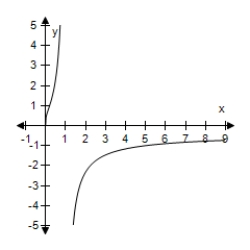
B) 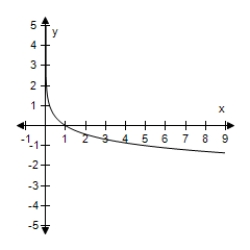
C) 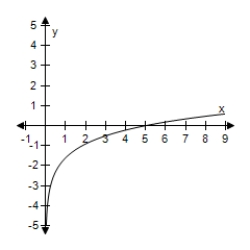
D) 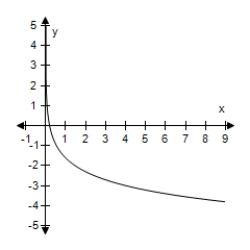
E) 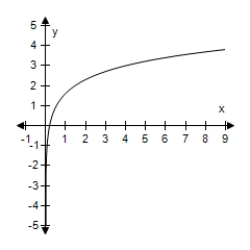
Correct Answer:

Verified
Correct Answer:
Verified
Related Questions
Q31: Condense the expression <span class="ql-formula"
Q32: Evaluate the logarithm using the change-of-base
Q33: Assume that x is a positive
Q34: Use the change-of-base formula to rewrite
Q35: Condense the expression <span class="ql-formula"
Q37: Find the exact value of
Q38: Find the exact value of
Q39: Find the exact value of
Q40: Use the properties of logarithms to
Q41: Assume that x,y,and z are positive