Multiple Choice
Use a graphing utility to graph the equation.Use the graph to approximate the values of x that satisfy each inequality.
Equation:
Inequality:
A) 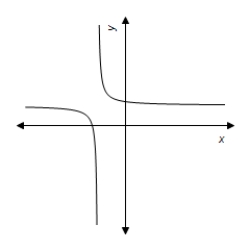
B) 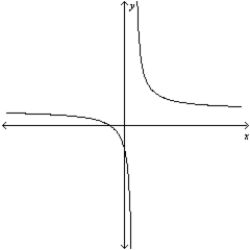
C) 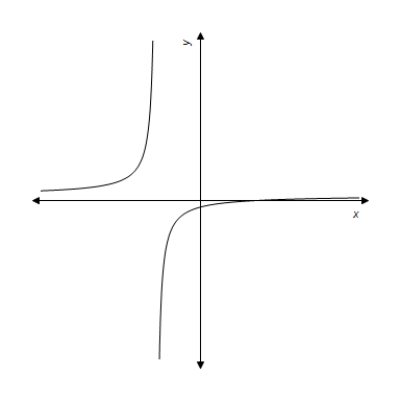
D) 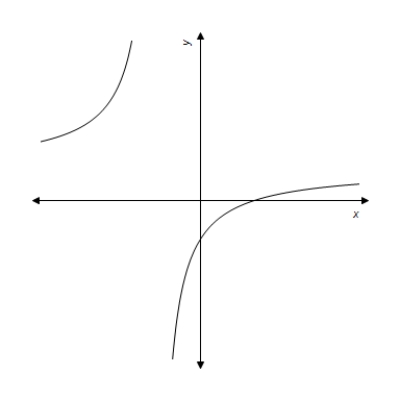
E) 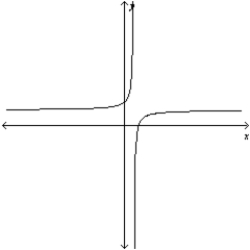
Correct Answer:

Verified
Correct Answer:
Verified
Related Questions
Q44: Solve the inequality and graph the
Q45: A rectangular playing field with a
Q46: Solve the inequality and write the
Q47: Solve the inequality and graph the
Q48: Use the position equation <span
Q50: Determine whether the value of
Q51: Solve the inequality and graph the
Q52: Solve the inequality and write the
Q53: Solve the inequality and graph the
Q54: Solve: <span class="ql-formula" data-value="x ^