Multiple Choice
Use the given value of k to complete the table for the direct variation model .
Plot the points on a rectangular coordinate system.
A)
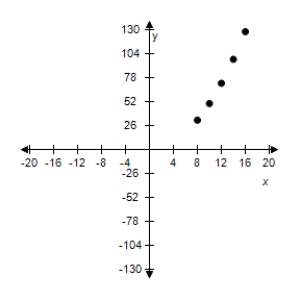
B)
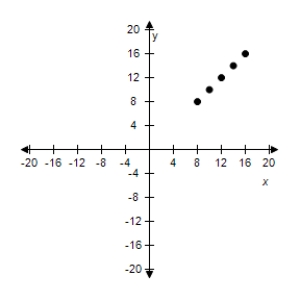
C)
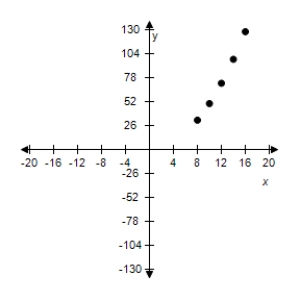
D)
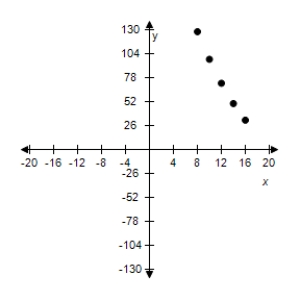
E)
Correct Answer:

Verified
Correct Answer:
Verified
Related Questions
Q1: State sales tax is based on
Q2: An overhead garage door has two
Q4: Use the given value of k
Q5: On a yardstick with scales in
Q6: Assume that y is directly proportional
Q7: Determine whether the variation model below
Q8: Find a mathematical model representing the
Q9: Determine whether the variation model is
Q10: Determine whether the variation model below
Q11: Find a mathematical model for the