Multiple Choice
Use the given value of k to complete the table for the inverse variation model Plot the points on a rectangular coordinate system.
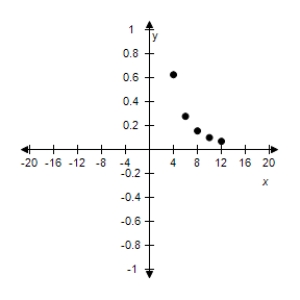
A)
B)
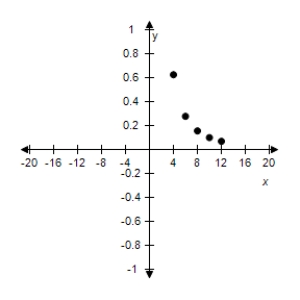
C)
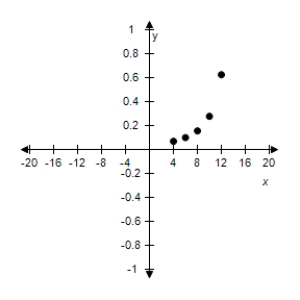
D)
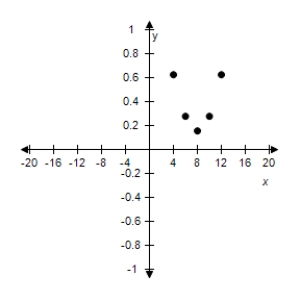
E)
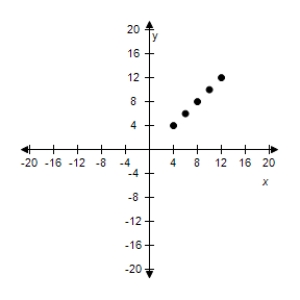
Correct Answer:

Verified
Correct Answer:
Verified
Related Questions
Q10: Determine whether the variation model below
Q11: Find a mathematical model for the
Q12: Find a mathematical model representing the
Q13: Assume that y is directly proportional
Q14: The coiled spring of a toy supports
Q16: When buying gasoline,you notice that 16
Q17: The sales tax on an item with
Q18: Use the fact that the diameter
Q19: Find a mathematical model for the
Q20: Use the given value of k