Multiple Choice
Select the parametric equations matching with the following graph. 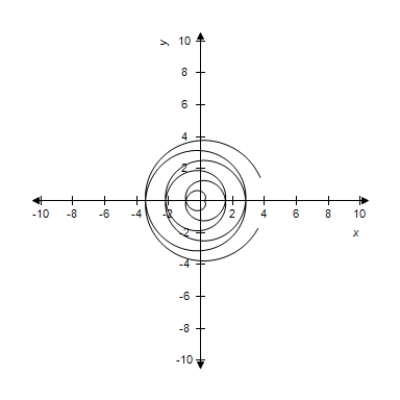
A) Involute of circle:
B) Involute of circle:
C) Involute of circle:
D) Involute of circle:
E) Involute of circle:
Correct Answer:

Verified
Correct Answer:
Verified
Related Questions
Q26: Select the curve represented by the
Q27: Find a set of parametric equations
Q28: Using following result find a set
Q29: Find a set of parametric equations
Q30: A projectile is launched at a
Q32: Select the curve represented by the
Q33: Eliminate the parameter and write the
Q34: Select the curve represented by the
Q35: Select the curve represented by the
Q36: Eliminate the parameter and write the