Solved

Consider the Following Calculations for a One-Way Analysis of Variance

Question 107

Multiple Choice

Consider the following calculations for a one-way analysis of variance from a completely randomized design with 20 total observations. MSE = 101.25 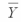Consider the following calculations for a one-way analysis of variance from a completely randomized design with 20 total observations. MSE = 101.25 <sub>overall</sub> = 39 <sub>1</sub> = 33 <sub>2</sub> = 43 <sub>3</sub> = 49 <sub>4</sub> = 31 Compute a 95% confidence interval for the second treatment mean. 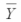A) (33.46 52.54) B) (30.51 55.49) C) (35.14 50.86) D) (22.75 63.25) overall = 39 Consider the following calculations for a one-way analysis of variance from a completely randomized design with 20 total observations. MSE = 101.25 <sub>overall</sub> = 39 <sub>1</sub> = 33 <sub>2</sub> = 43 <sub>3</sub> = 49 <sub>4</sub> = 31 Compute a 95% confidence interval for the second treatment mean. 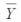A) (33.46 52.54) B) (30.51 55.49) C) (35.14 50.86) D) (22.75 63.25) 1 = 33 Consider the following calculations for a one-way analysis of variance from a completely randomized design with 20 total observations. MSE = 101.25 <sub>overall</sub> = 39 <sub>1</sub> = 33 <sub>2</sub> = 43 <sub>3</sub> = 49 <sub>4</sub> = 31 Compute a 95% confidence interval for the second treatment mean. A) (33.46 52.54) B) (30.51 55.49) C) (35.14 50.86) D) (22.75 63.25) 2 = 43 Consider the following calculations for a one-way analysis of variance from a completely randomized design with 20 total observations. MSE = 101.25 <sub>overall</sub> = 39 <sub>1</sub> = 33 <sub>2</sub> = 43 <sub>3</sub> = 49 <sub>4</sub> = 31 Compute a 95% confidence interval for the second treatment mean. A) (33.46 52.54) B) (30.51 55.49) C) (35.14 50.86) D) (22.75 63.25) 3 = 49 Consider the following calculations for a one-way analysis of variance from a completely randomized design with 20 total observations. MSE = 101.25 <sub>overall</sub> = 39 <sub>1</sub> = 33 <sub>2</sub> = 43 <sub>3</sub> = 49 <sub>4</sub> = 31 Compute a 95% confidence interval for the second treatment mean. A) (33.46 52.54) B) (30.51 55.49) C) (35.14 50.86) D) (22.75 63.25) 4 = 31
Compute a 95% confidence interval for the second treatment mean.


A) (33.46 52.54)
B) (30.51 55.49)
C) (35.14 50.86)
D) (22.75 63.25)

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q48: The error sum of squares measures the

Q80: _ simultaneous confidence intervals test all of

Q94: Different levels of a factor are called

Q102: Consider the following partial analysis of variance

Q103: A company that fills gallon containers of

Q105: A company that fills gallon containers of

Q106: Consider the following partial analysis of variance

Q109: Consider the following partial analysis of variance

Q110: A company that fills gallon containers

Q113: In a completely randomized (one-way) analysis of