Solved

Suppose That a Population Develops According to the Logistic Equation

Question 5

Multiple Choice

Suppose that a population develops according to the logistic equation Suppose that a population develops according to the logistic equation , where t is measured in weeks. What is the carrying capacity? A) B) C) D) E) , where t is measured in weeks. What is the carrying capacity?


A) Suppose that a population develops according to the logistic equation , where t is measured in weeks. What is the carrying capacity? A) B) C) D) E)
B) Suppose that a population develops according to the logistic equation , where t is measured in weeks. What is the carrying capacity? A) B) C) D) E)
C) Suppose that a population develops according to the logistic equation , where t is measured in weeks. What is the carrying capacity? A) B) C) D) E)
D) Suppose that a population develops according to the logistic equation , where t is measured in weeks. What is the carrying capacity? A) B) C) D) E)
E) Suppose that a population develops according to the logistic equation 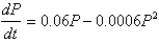, where t is measured in weeks. What is the carrying capacity? A) 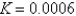B) 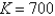C) 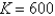D) E)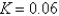

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q1: A population is modeled by the differential

Q2: Suppose that a population grows according to

Q3: Which of the following functions is a

Q4: A function <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5971/.jpg" alt="A function

Q6: A sum of <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5971/.jpg" alt="A sum

Q7: Use Euler's method with step size 0.25

Q8: Determine whether the differential equation is linear.

Q9: Solve the initial-value problem. <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5971/.jpg" alt="Solve

Q10: A curve passes through the point <img

Q11: Find the solution of the differential equation