Solved

Suppose That a Population Grows According to a Logistic Model

Question 49

Multiple Choice

Suppose that a population grows according to a logistic model with carrying capacity Suppose that a population grows according to a logistic model with carrying capacity and per year. Choose the logistic differential equation for these data. A) B) C) D) E) and Suppose that a population grows according to a logistic model with carrying capacity and per year. Choose the logistic differential equation for these data. A) B) C) D) E) per year. Choose the logistic differential equation for these data.


A) Suppose that a population grows according to a logistic model with carrying capacity and per year. Choose the logistic differential equation for these data. A) B) C) D) E)
B) Suppose that a population grows according to a logistic model with carrying capacity and per year. Choose the logistic differential equation for these data. A) B) C) D) E)
C) Suppose that a population grows according to a logistic model with carrying capacity and per year. Choose the logistic differential equation for these data. A) B) C) D) E)
D) Suppose that a population grows according to a logistic model with carrying capacity and per year. Choose the logistic differential equation for these data. A) B) C) D) E)
E) Suppose that a population grows according to a logistic model with carrying capacity and 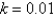per year. Choose the logistic differential equation for these data. A) B) C) D) 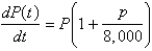E)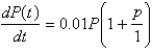

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q44: Let c be a positive number. A

Q45: Solve the differential equation. <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5971/.jpg" alt="Solve

Q46: Kirchhoff's Law gives us the derivative equation

Q47: The population of the world was about

Q48: Solve the initial-value problem. <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5971/.jpg" alt="Solve

Q50: An object with mass m is dropped

Q51: The solution of the differential equation <img

Q52: In the circuit shown in Figure, a

Q53: Let <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5971/.jpg" alt="Let be

Q54: Select a direction field for the differential