Multiple Choice
Find the inverse of F. Then sketch the graphs of f and f -1 on the same set of axes.f (x) = 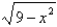 , x 0
, x 0
A) f -1(x) = - 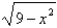 , x 0
, x 0 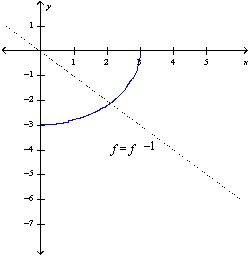
B) f -1(x) = 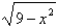 , x 0
, x 0 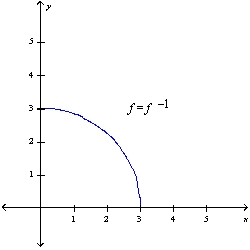
C) f -1(x) = 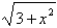 , x 0
, x 0 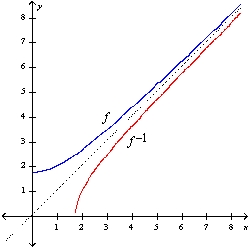
D) f -1(x) = - 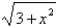 , x 0
, x 0 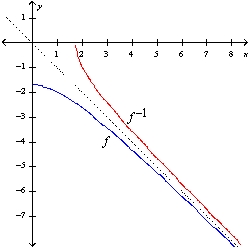
Correct Answer:

Verified
Correct Answer:
Verified
Q43: If a bacteria population starts with 50
Q44: Strontium- <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5971/.jpg" alt="Strontium- has
Q45: Use the laws of logarithms to write
Q46: Use logarithmic differentiation to find the derivative
Q47: Find f <sup>-</sup><sup>1 </sup>(a) for the function
Q49: Use Newton's method to find the roots
Q50: Find the limit. <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5971/.jpg" alt="Find the
Q51: Write the expression as an exponent with
Q52: Find the derivative of <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5971/.jpg" alt="Find
Q53: Find the inverse of the function. <img