Short Answer
Use Newton's method to approximate the indicated root of 
in the interval 
, correct to six decimal places.
Use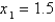 
as the initial approximation.
Correct Answer:
Verified
Correct Answer:
Verified
Q18: To what constant deceleration would a car
Q19: Find the limit. <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5971/.jpg" alt="Find the
Q21: Find the inflection points for the function
Q22: Sketch the curve. <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5971/.jpg" alt="Sketch the
Q24: Find the absolute maximum value of <img
Q25: Find the maximum and minimum points of
Q26: A skydiver leaps from a helicopter hovering
Q27: The altitude (in feet) attained by a
Q28: Find a cubic function <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5971/.jpg" alt="Find
Q133: Find two numbers whose difference is 170