Multiple Choice
A rectangular beam will be cut from a cylindrical log of radius 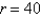 inches. Suppose that the strength of a rectangular beam is proportional to the product of its width and the square of its depth. Find the dimensions of the strongest beam that can be cut from the cylindrical log.
inches. Suppose that the strength of a rectangular beam is proportional to the product of its width and the square of its depth. Find the dimensions of the strongest beam that can be cut from the cylindrical log. 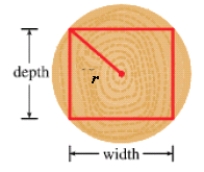
A) 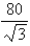 in,
in, 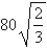 in
in
B) 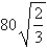 in,
in, 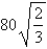 in
in
C) 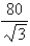 in,
in, 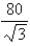 in
in
D) 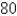 in,
in,  in
in
E)  in,
in, 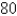 in
in
Correct Answer:

Verified
Correct Answer:
Verified
Q120: Use Newton's method to find the zero
Q121: Sketch the graph of the function <img
Q122: The graph of the derivative <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5971/.jpg"
Q123: You are given the graph of a
Q124: You are given the graph of the
Q126: Determine where the graph of the function
Q127: Find the critical numbers of the function.
Q128: Find f. <br><img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5971/.jpg" alt="Find f.
Q129: How many real roots does the equation
Q130: Estimate the value of <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5971/.jpg" alt="Estimate