Solved

Suppose That F and G Are Functions That Are Differentiable

Question 56

Short Answer

Suppose that f and g are functions that are differentiable at x = 1 and that f (1) = 1, Suppose that f and g are functions that are differentiable at x = 1 and that f (1) = 1, (1) = -2, g (1) = 3, and (1) = 4. Find . (1) = -2, g (1) = 3, and 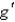Suppose that f and g are functions that are differentiable at x = 1 and that f (1) = 1, (1) = -2, g (1) = 3, and (1) = 4. Find . (1) = 4. Find Suppose that f and g are functions that are differentiable at x = 1 and that f (1) = 1, (1) = -2, g (1) = 3, and (1) = 4. Find . . Suppose that f and g are functions that are differentiable at x = 1 and that f (1) = 1, (1) = -2, g (1) = 3, and (1) = 4. Find .

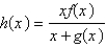
Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q51: Find the linearization L (x) of the

Q52: Find <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5971/.jpg" alt="Find .

Q53: Find the limit. <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5971/.jpg" alt="Find the

Q54: Find an equation of the tangent line

Q55: Find an equation of the tangent line

Q57: If <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5971/.jpg" alt="If " class="answers-bank-image

Q58: Determine the constants A, B, and C

Q59: Find the tangent line to the parabola

Q60: The top of a ladder slides down

Q61: Find the derivative of the function.<br>f (x)