Solved

A Box with an Open Top Is to Be Constructed

Question 45

Multiple Choice

A box with an open top is to be constructed from a rectangular piece of card board with dimensions A box with an open top is to be constructed from a rectangular piece of card board with dimensions in. by in. by cutting out equal squares of side x at each corner and then folding up the sides as in the figure. Express the volume V of the box as a function of x. A) B) C) D) E) in. by A box with an open top is to be constructed from a rectangular piece of card board with dimensions in. by in. by cutting out equal squares of side x at each corner and then folding up the sides as in the figure. Express the volume V of the box as a function of x. A) B) C) D) E) in. by cutting out equal squares of side x at each corner and then folding up the sides as in the figure. Express the volume V of the box as a function of x. A box with an open top is to be constructed from a rectangular piece of card board with dimensions in. by in. by cutting out equal squares of side x at each corner and then folding up the sides as in the figure. Express the volume V of the box as a function of x. A) B) C) D) E)


A) A box with an open top is to be constructed from a rectangular piece of card board with dimensions in. by in. by cutting out equal squares of side x at each corner and then folding up the sides as in the figure. Express the volume V of the box as a function of x. A) B) C) D) E)
B) A box with an open top is to be constructed from a rectangular piece of card board with dimensions in. by in. by cutting out equal squares of side x at each corner and then folding up the sides as in the figure. Express the volume V of the box as a function of x. A) B) C) D) E)
C) A box with an open top is to be constructed from a rectangular piece of card board with dimensions in. by in. by cutting out equal squares of side x at each corner and then folding up the sides as in the figure. Express the volume V of the box as a function of x. A) B) C) D) E)
D) A box with an open top is to be constructed from a rectangular piece of card board with dimensions in. by in. by cutting out equal squares of side x at each corner and then folding up the sides as in the figure. Express the volume V of the box as a function of x. A) B) C) D) E)
E) A box with an open top is to be constructed from a rectangular piece of card board with dimensions 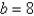in. by 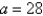in. by cutting out equal squares of side x at each corner and then folding up the sides as in the figure. Express the volume V of the box as a function of x. A) 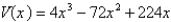B) 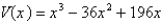C) 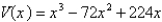D) E)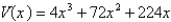

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q40: Determine whether the function whose graph is

Q41: Use continuity to evaluate the limit. <img

Q42: Use the graph to determine where the

Q43: The monthly cost of driving a car

Q44: Find the limit <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5971/.jpg" alt="Find the

Q46: A tank holds <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5971/.jpg" alt="A tank

Q47: Find the limit. <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5971/.jpg" alt="Find the

Q48: Use the graph of the function to

Q49: The graphs of <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5971/.jpg" alt="The graphs

Q50: Find the limit. <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5971/.jpg" alt="Find the