Solved

When We Test H0: μ1 − μ2 £ 0,HA: μ1

Question 40

Essay

When we test H0: μ1 − μ2 £ 0,HA: μ1 − μ2 > 0,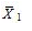
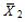When we test H<sub>0</sub>: μ<sub>1</sub> − μ<sub>2</sub> £ 0,H<sub>A</sub>: μ<sub>1</sub> − μ<sub>2</sub> > 0, = 15.4, = 14.5,s<sub>1</sub> = 2,s<sub>2</sub> = 2.28,n<sub>1</sub> = 35,and n<sub>2</sub> = 18 at α = .01,can we reject the null hypothesis? (Assume unequal variances. )= 15.4,
When we test H<sub>0</sub>: μ<sub>1</sub> − μ<sub>2</sub> £ 0,H<sub>A</sub>: μ<sub>1</sub> − μ<sub>2</sub> > 0, = 15.4, = 14.5,s<sub>1</sub> = 2,s<sub>2</sub> = 2.28,n<sub>1</sub> = 35,and n<sub>2</sub> = 18 at α = .01,can we reject the null hypothesis? (Assume unequal variances. )= 14.5,s1 = 2,s2 = 2.28,n1 = 35,and n2 = 18 at α = .01,can we reject the null hypothesis? (Assume unequal variances. )

Correct Answer:

verifed

Verified

No.Cannot reject the null hypo...

View Answer

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q4: Parameters of the F distribution include<br>A) n<sub>1</sub>.<br>B)

Q5: In testing the equality of population variance,

Q37: In order to test the effectiveness of

Q37: There are two types of machines,called type

Q41: Find a 95 percent confidence interval for

Q42: Find a 95 percent confidence interval for

Q43: In testing the difference between two independent

Q44: In testing the difference between the means

Q75: If the limits of the confidence interval

Q136: When we are testing a hypothesis about