Solved

For the Quadratic Regression Equation ,The Predicted Y Achieves

Question 39

Multiple Choice

For the quadratic regression equation For the quadratic regression equation ,the predicted y achieves its optimum (maximum or minimum) when x is: A) B) C) D) ,the predicted y achieves its optimum (maximum or minimum) when x is:


A) For the quadratic regression equation ,the predicted y achieves its optimum (maximum or minimum) when x is: A) B) C) D)
B) For the quadratic regression equation ,the predicted y achieves its optimum (maximum or minimum) when x is: A) B) C) D)
C) For the quadratic regression equation ,the predicted y achieves its optimum (maximum or minimum) when x is: A) B) C) D)
D) For the quadratic regression equation 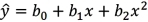,the predicted y achieves its optimum (maximum or minimum) when x is: A) 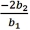B) 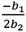C) 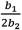D)

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q5: Which of the following regression models is

Q34: Exhibit 16-7.It is believed that the sales

Q35: An inverted U-shaped curve is also known

Q38: Exhibit 16-7.It is believed that the sales

Q41: Exhibit 16.6.Thirty employed single individuals were randomly

Q43: For the exponential model ln(y)= β<sub>0</sub> +

Q44: Exhibit 16-4.The following data shows the cooling

Q48: A model with one explanatory variable being

Q58: Although a polynomial regression model of order

Q68: The regression model ln(y)= β<sub>0</sub> + β<sub>1</sub>x