Solved

The Fundamental Frequency of a Vibrating String Is F1

Question 36

Multiple Choice

The fundamental frequency of a vibrating string is f1. If the tension in the string is doubled, the fundamental frequency becomes


A) 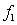The fundamental frequency of a vibrating string is f<sub>1</sub>. If the tension in the string is doubled, the fundamental frequency becomes A) <sub> </sub>/2 B) C) D) E) 2 /2
B) 11eaa4be_8550_d4cd_9e4a_9b9f5c46c44e_TB6080_11 11eaa4be_8550_fbde_9e4a_d7ed8083361c_TB6080_11
C) 11eaa4be_8550_d4cd_9e4a_9b9f5c46c44e_TB6080_11
D) 11eaa4be_8550_fbdf_9e4a_25d12c5de7d6_TB6080_11
E) 211eaa4be_8550_d4cd_9e4a_9b9f5c46c44e_TB6080_11

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q34: <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB6080/.jpg" alt=" The frequency spectrum

Q35: <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB6080/.jpg" alt=" The figure shows

Q37: <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB6080/.jpg" alt=" The figure represents

Q39: <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB6080/.jpg" alt=" The figure shows

Q41: <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB6080/.jpg" alt="

Q51: A vibrating tuning fork of frequency 1080

Q59: A vibrating tuning fork of frequency 640

Q71: Two waves with the same frequency and

Q78: What is the third harmonic of an

Q82: A string fixed at both ends is