Multiple Choice
Find a first-degree polynomial function P1 whose value and slope agree with the value and slope of f at  . What is P1 called?
. What is P1 called? 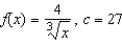
A) 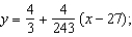 tangent line to
tangent line to 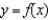 at
at 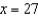
B) 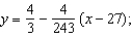 secant line to
secant line to 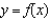 at
at 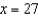
C) 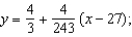 secant line to
secant line to 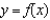 at
at 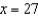
D)  secant line to
secant line to 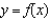 at
at 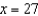
E) 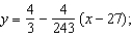 tangent line to
tangent line to 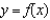 at
at 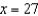
Correct Answer:

Verified
Correct Answer:
Verified
Q1: Find the Maclaurin polynomial of degree 5
Q2: Determine the values of x for which
Q4: Find the Maclaurin polynomial of degree 4
Q5: What is <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB4584/.jpg" alt="What is
Q6: Find a first-degree polynomial function P<sub>1</sub> whose
Q7: Determine the degree of the Maclaurin polynomial
Q8: Find the fourth degree Taylor polynomial centered
Q9: Find the fourth degree Maclaurin polynomial for
Q10: Find the Maclaurin polynomial of degree two
Q11: Consider the function <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB4584/.jpg" alt="Consider the