Solved

The Logistic Function Models the Growth of a Population

Question 7

Multiple Choice

The logistic function 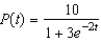The logistic function models the growth of a population. Determine when the population reaches one-half of the maximum carrying capacity. Round your answer to three decimal places. A) 0.549 B) 3.333 C) 1.151 D) 5.000 E) 1.000 models the growth of a population. Determine when the population reaches one-half of the maximum carrying capacity. Round your answer to three decimal places.


A) 0.549
B) 3.333
C) 1.151
D) 5.000
E) 1.000

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q2: Find the logistic equation that satisfies the

Q3: Each of the following graphs is from

Q4: Match the logistic equation and initial condition

Q5: A conservation organization releases 30 panthers into

Q6: The logistic function <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB4584/.jpg" alt="The logistic

Q8: The logistic function <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB4584/.jpg" alt="The logistic

Q9: Identify the graph of the logistic function

Q10: A conservation organization releases 40 coyotes into

Q11: Match the logistic differential equation and initial

Q12: The logistic function <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB4584/.jpg" alt="The logistic