Solved

The Solid in the First Octant Bounded by the Sphere

Question 58

Essay

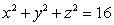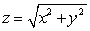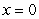The solid in the first octant bounded by the sphere The solid in the first octant bounded by the sphere above, by the cone below, and by the planes and on the side, has a density . Set up the integral for the mass of the solid A) in rectangular coordinates. B) in cylindrical coordinates. C) in spherical coordinates. above, by the cone The solid in the first octant bounded by the sphere above, by the cone below, and by the planes and on the side, has a density . Set up the integral for the mass of the solid A) in rectangular coordinates. B) in cylindrical coordinates. C) in spherical coordinates. 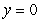below, and by the planes The solid in the first octant bounded by the sphere above, by the cone below, and by the planes and on the side, has a density . Set up the integral for the mass of the solid A) in rectangular coordinates. B) in cylindrical coordinates. C) in spherical coordinates. 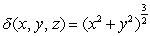and The solid in the first octant bounded by the sphere above, by the cone below, and by the planes and on the side, has a density . Set up the integral for the mass of the solid A) in rectangular coordinates. B) in cylindrical coordinates. C) in spherical coordinates. on the side, has a density The solid in the first octant bounded by the sphere above, by the cone below, and by the planes and on the side, has a density . Set up the integral for the mass of the solid A) in rectangular coordinates. B) in cylindrical coordinates. C) in spherical coordinates. .
Set up the integral for the mass of the solid
A) in rectangular coordinates.
B) in cylindrical coordinates.
C) in spherical coordinates.

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q53: The value of the integral <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5596/.jpg"

Q54: Find the volume of the region under

Q55: Let <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5596/.jpg" alt="Let where

Q56: Given the integral <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5596/.jpg" alt="Given the

Q57: Calculate the probability that <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5596/.jpg" alt="Calculate

Q59: Evaluate <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5596/.jpg" alt="Evaluate ,

Q60: Integrate <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5596/.jpg" alt="Integrate over

Q61: The volume of the ellipsoid <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5596/.jpg"

Q62: Consider a flat plate occupying the region

Q63: Find the volume of the solid bounded