Multiple Choice
The equation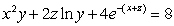 
defines the function 
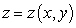near the point 
.
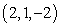The point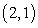 
is:
A) a local maximum of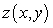 
.
B) a local minimum of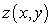 
.
C) a saddle point of 
.
D) a global maximum of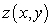 
.
E) not a critical point of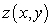 
.
Correct Answer:
Verified
Correct Answer:
Verified
Q53: If <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5596/.jpg" alt="If ,
Q54: Determine whether the following function is continuous.
Q55: Find all the functions <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5596/.jpg" alt="Find
Q56: The maximum value of <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5596/.jpg" alt="The
Q57: Find the level curves of the function
Q59: Describe and sketch the level curves of
Q60: Evaluate the limit or state that it
Q61: Find the tangent plane to the graph
Q62: Find the distance to the origin from
Q63: Given that <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5596/.jpg" alt="Given that