Multiple Choice
Let 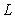 be the intersection curve between the surfaces
be the intersection curve between the surfaces 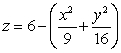 and
and 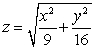 .
.
If  ,
, 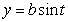 , and
, and  is a parameterization of
is a parameterization of  then:
then:
A) 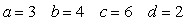
B) 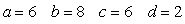
C) 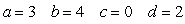
D) 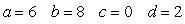
E)  cannot be parameterized by a parameterization in this form.
cannot be parameterized by a parameterization in this form.
Correct Answer:

Verified
Correct Answer:
Verified
Related Questions
Q37: Find the length of the curve described
Q38: Describe the curve traced by the following
Q39: A particle's position at time <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5596/.jpg"
Q40: Find an arc length parametrization of the
Q41: The path of a projectile is parametrized
Q43: The aphelion (farthest distance from the Sun)
Q44: The angular momentum in kg m<sup>2</sup>/s of
Q45: Find the tangent line to the curve
Q46: Parametrize the tangent line to the curve
Q47: Find a parametric equation for the tangent