Solved

Let Be a Sequence Such That

Question 49

Short Answer

Let 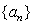Let be a sequence such that . Use the definition of the limit and the Squeeze Theorem to find . be a sequence such that Let be a sequence such that . Use the definition of the limit and the Squeeze Theorem to find . .
Use the definition of the limit and the Squeeze Theorem to find Let be a sequence such that 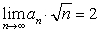. Use the definition of the limit and the Squeeze Theorem to find . .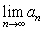

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q44: Find the Maclaurin series for <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5596/.jpg"

Q45: Does the series <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5596/.jpg" alt="Does the

Q46: Use the Integral Test to determine if

Q47: Find the partial sums of the series

Q48: Determine whether the series is absolutely convergent,

Q50: Determine whether the series <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5596/.jpg" alt="Determine

Q51: Determine if the following series converge.<br>A) <img

Q52: Use the formula for geometric series to

Q53: Determine if the following series is conditionally

Q54: Which of the following series is conditionally