Solved

The Horizontal Cross Sections at Height of a Tank

Question 68

Short Answer

The horizontal cross sections at height The horizontal cross sections at height of a tank are discs of radius . The height of the tank is 10 m. The tank is filled with water, and the water drains through a square hole with a side of 10 cm at the bottom of the tank. How long does it take for the tank to empty? of a tank are discs of radius The horizontal cross sections at height of a tank are discs of radius . The height of the tank is 10 m. The tank is filled with water, and the water drains through a square hole with a side of 10 cm at the bottom of the tank. How long does it take for the tank to empty? . The height of the tank is 10 m.
The tank is filled with water, and the water drains through a square hole with a side of 10 cm at the bottom of the tank.
How long does it take for the tank to empty? The horizontal cross sections at height 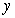of a tank are discs of radius 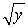. The height of the tank is 10 m. The tank is filled with water, and the water drains through a square hole with a side of 10 cm at the bottom of the tank. How long does it take for the tank to empty?

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q63: A rat population in a certain field

Q64: A certain chemical dissolves in water at

Q65: Use the following steps.<br>A) Write an equation

Q66: Solving the differential equation <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5596/.jpg" alt="Solving

Q67: Find all curves <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5596/.jpg" alt="Find all

Q69: A deer population for a certain area

Q70: Match the differential equation with its slope

Q71: Consider the logistic equation <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5596/.jpg" alt="Consider

Q72: Match the differential equation with its slope

Q73: Solve the initial value problem <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5596/.jpg"